Replicating portfolio for bonds cash flow as per FRM CFA Exam

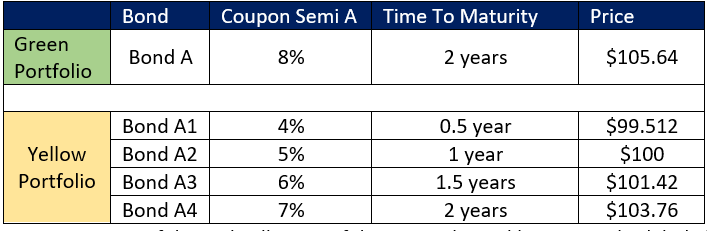
We discussed in law of one price, if two portfolios provide same cashflows then it should be priced at same level. In this section we will see how to create portfolio which mimicking the cash flow of another portfolio. Assume we have Portfolio Green consists of a bond (Face value $100) currently priced at $105.64 , pays coupon of 8% semi annual and time to maturity is 2 years (4 periods). (See diagram given below). Assume we have 4 bonds (given in table below) to create replicating portfolio  call it a yellow portfolio which mimics the cash flow of green portfolio. Because both the portfolios provide same cashflows, we can say the price should be same.

Note: For the pricing of these bonds semi annual yield of 5% and face value of $100 is assumed and all prices can be derived using TI BA II Plus calculator TVM Function.

Note: Green portfolio and yellow portfolios are indicated by same color labels (of bond name) in following figure for easy review.

Following diagram shows the percentage of face value required from each bond to create a replicating portfolio(yellow) which mimics the cash flow of green portfolio. In this section we will learn how to calculate the percentage of face value in later part. First lets focus on how the replicating portfolio works. We have bond A which pays coupon of 8% semi annual, which means after every 6 months coupon of $4 will be received and at the end of 24 months coupon with face value amounting to $104 is received. Lets consider the last cash flow of $104 from green portfolio. If we have to mimic this cash flow the only option we have is Bond A4 which matures in 24 months. Bond A1 to A3 are of no use because these bonds are maturing before 24 months. We can see in the following diagram Bond A4 needs 100.48% of face value to get same cash flow as Bond A’s at the end of 24 month. Bond A4s cash flow at the end of 24^th month with face value of $100 is 103.5. But we made investment equal to 100.48% of face value, hence Bond A4s cash flow on invested amount is $103.5 X 100.48% = $104. This cash flow is same as cash flow from green portfolio of Bond A in 24^th month. However, the investment in Bond A4 is generating cash flow for all periods including periods prior to 24^th month which creates overlap with other Bonds A1 to A3. Now consider 18^th month cash flow. In this month the combined cash flow $4 from Bond A3 and A4 is equal to cash flow of Bond A. In this case Bond A4 substantially contributes to the cash flow. Total investment in Bond A3 is 0.469% of face value. Hence cash flow from Bond A3 in 18^th month is $0.483 (0.469% of $103.00)

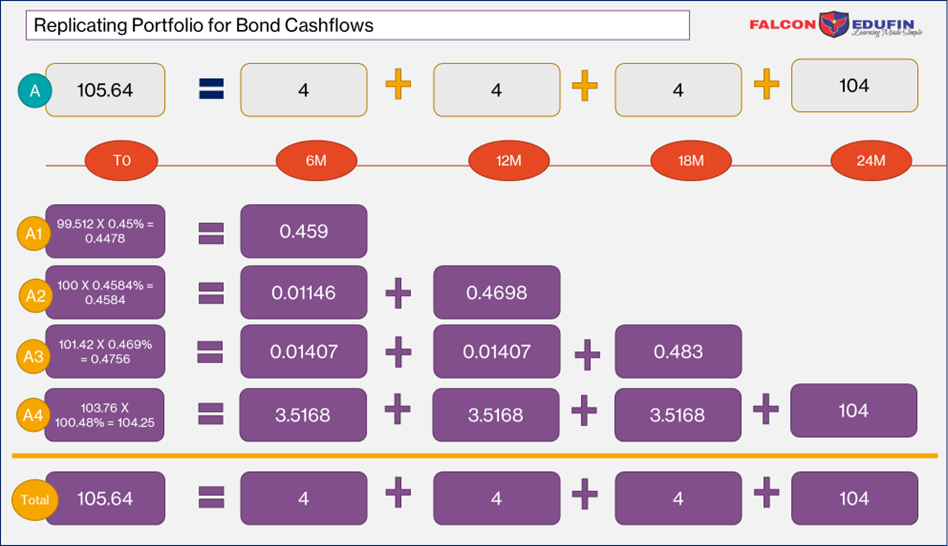
Bond A4: To calculate the percentage of face value (FA4) we have to start with Bond A4. Best method is to start with matching cash flow of maturity month of every bond. Hence for bond A4 we will match the cash flow of Bond A = $104 and Bond A4 = FV4 X 103.5.

FA4 X 103.5 = 104 X 100, Solving this equation gives us

FA4 = 100.48%

104 is multiplied by 100 to calculate percentage of face value. Same will be applicable for all the following calculations.

For Bond A3, we have to match only coupon cash flow from bond A = $4 in 18^th month with cash flow of Bond A3 face value cash flow 103. However, we also have cash flow from Bond A4 in 18^th month which needs to be adjusted in equation.

FA3 X 103 + 100.48% of 3.5 = $4 X 100

FA3 = 0.469%

Similarly for Bond A2:

FA2 X 102.5 + 3 X 0.469% + 3.5 X 100.48% = 4 X 100

FA2 = 0.4584%

For Bond A1

FA1 X 102 + 2.5 X 0.4584% + 3 X 0.469% + 3.5X 100.48%

FA1 = 0.45%

To calculate cash flows for respective bonds, simply multiply every bonds cash flow with percentage of face value. Also the investment value is price of each bond multiplied by percentage of investment calculated above.

Arbitrage opportunity

If say green portfolio is selling at lower price than yellow portfolio, arbitrage exists. To exploit the arbitrage opportunity trader will take the long position in cheaper portfolio and short position in expensive portfolio to generate fixed risk free profit. This will create demand side pressure for cheaper portfolio and supply side pressure for expensive portfolio, will result in price increase cheaper portfolio and price decrease for expensive portfolio. Hence, the arbitrage will force the price of both the portfolios to be equal.