C02 CALCULATING AND APPLYING VAR

DEFINATION #

Value at risk (VaR) is a probabilistic method of measuring the potential loss in portfolio value over a given time period and for a given distribution of historical returns. There is an X percent probability that the loss in portfolio value will be equal to or greater than the VaR measure.

CALCULATING VAR

Calculating delta-normal VaR requires assuming that asset returns conform to a standard normal distribution. A standard normal distribution is defined by two parameters, its mean (|i = 0) and standard deviation (a = 1), and is perfectly symmetric with 50% of the distribution lying to the right of the mean and 50% lying to the left of the mean.

VaR (X%) = zx% σ

Where:

VaR (X%) =  the X% probability value at risk

zx%  =  the critical z-value based on the normal distribution and the selected X% probability.

σ = the standard deviation of daily returns on a percentage basis.

VaR CONVERSIONS #

Risk managers may be interested in measuring risk over longer time periods, such as a month, quarter, or year. VaR can be converted from a 1-day basis to a longer basis by multiplying the daily VaR by the square root of the number of days (J) in the longer time period (called the square root rule).

For example, to convert to a weekly VaR, multiply the daily VaR by the square root of 5 (i.e., five business days in a week). We can generalize the conversion method as follows:

VaR(X%)J-days = VaR(X%)1-day     J

THE VaR METHODS #

LINEAR METHODS:   Linear methods replace portfolio positions with linear exposures on the appropriate risk factor.

• The Delta Normal Valuation Method : The delta-normal approach begins by valuing the portfolio at an initial point as a relationship to a specific risk factor, S (consider only one risk factor exists):

v₀ = V(S₀)

With this expression, we can describe the relationship between the change in portfolio value and the change in the risk factor as:

                                 dV = Δ₀ x dS

Here,  Δ0 is the sensitivity of the portfolio to changes in the risk factor, S. As with any linear relationship, the biggest change in the value of the portfolio will accompany the biggest change in the risk factor. The VaR at a given level of significance, z, can be written as:

VaR = |Δ₀| x (zσS₀)

The delta-normal method for estimating VaR requires the assumption of a normal distribution. This is because the method utilizes the expected return and standard deviation of returns.

Advantages of the delta-normal VaR method

• Easy to implement.
• Calculations can be performed quickly.
• Conducive to analysis because risk factors, correlations, and volatilities are identified.

Disadvantages of the delta-normal method

• The need to assume a normal distribution.
• The method is unable to properly account for distributions with fat tails, either because of unidentified time variation in risk or unidentified risk factors and/or correlations.
• Nonlinear relationships of option-like positions are not adequately described by the delta-normal method. VaR is misstated because the instability of the option deltas is not captured.

2. FULL VALUATION METHODS : The full valuation approaches provide the most accurate measurements because they include all nonlinear relationships and other potential correlations that may not be included in the linear valuation models.

• Historical Simulation Method : The easiest way to calculate the 5% daily VaR using the historical method is to accumulate a number of past daily returns, rank the returns from highest to lowest, and identify the lowest 5% of returns. The highest of these lowest 5% of returns is the 1-day, 5% VaR.

Advantages of the historical simulation method

• The model is easy to implement.
• Calculations are simple and can be performed quickly.
• Horizon is a positive choice based on the intervals of historical data used.
• Full valuation of portfolio is based on actual prices.
• It is not exposed to model risk.
• It includes all correlations as embedded in market price changes.

Disadvantages of the historical simulation method

• It may not be enough historical data for all assets.
• Only one path of events is used (the actual history), which includes changes in correlations and volatilities that may have occurred only in that historical period.
• Time variation of risk in the past may not represent variation in the future.
• The model may not recognize changes in volatility and correlations from structural changes.
• It is slow to adapt to new volatilities and correlations as old data carries the same weight as more recent data.
• A small number of actual observations may lead to insufficiently defined distribution tails
• Monte Carlo Simulation Method : The Monte Carlo method refers to computer software that generates hundreds, thousands, or even millions of possible outcomes from the distributions of inputs specified by the user for return on the portfolio. The several thousand weighted average portfolio returns will naturally form a distribution, which will approximate the normal distribution. Using the portfolio expected return and the standard deviation, which are part of the Monte Carlo output, VaR is calculated in the same way as with the delta-normal method.

Advantages of the Monte Carlo method

• It is the most powerful model.
• It can account for both linear and nonlinear risks.
• It can include time variation in risk and correlations by aging positions over chosen horizons.
• It is extremely flexible and can incorporate additional risk factors easily.
• Nearly unlimited numbers of scenarios can produce well-described distributions.

Disadvantages of the Monte Carlo method

• There is a lengthy computation time as the number of valuations escalates quickly.
• It is expensive because of the intellectual and technological skills required.
• It is subject to model risk of the stochastic processes chosen.
• It is subject to sampling variation at lower numbers of simulations.

DEVIATION FROM THE NORMAL DISTRIBUTION #

Three common deviations from normality that are problematic in modelling risk result from asset returns that are fat-tailed, skewed, or unstable.

• Fat-tailed refers to a distribution with a higher probability of observations occurring in the tails relative to the normal distribution.
• A distribution is skewed when the distribution is not symmetrical and there is a higher probability of outliers.
• Parameters of the model that vary over time are said to be unstable.
• The phenomenon of “fat tails” is most likely the result of the volatility and/or the mean of the distribution changing over time. If the mean and standard deviation are the same for asset returns for any given day, the distribution of returns is referred to as an unconditional distribution of asset returns. However, different market or economic conditions may cause the mean and variance of the return distribution to change over time. In such cases, the return distribution is referred to as a conditional distribution.

The second possible explanation for “fat tails” is that the second moment or volatility is time-varying. This explanation is much more likely given observed changes in interest rate volatility. Increased market uncertainty following significant political or economic events results in increased volatility of return distribution.

MARKET REGIMES & CONDITIONAL DISTRIBUTIONS #

• A regime-switching volatility model assumes different market regimes exist with high or low volatility. The conditional distributions of returns are always normal with a constant mean but either have a high or low volatility.
• The probability of large deviations from normality occurring are much less likely under the regime-switching model. The regime-switching model captures the conditional normality and may resolve the fat-tail problem and other deviations from normality.

VAR APPROACHES #

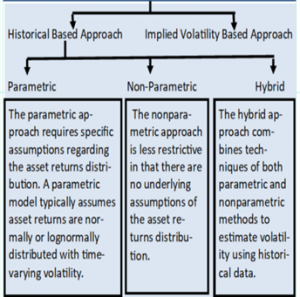
PARAMETRIC APPROACHES FOR VAR #

• The RiskMetrics® [i.e., exponentially weighted moving average (EWMA) model] and GARCH approaches are both exponential smoothing weighting methods. RiskMetrics® is actually a special case of the GARCH approach.
• The historical standard deviation approach assumes all K returns in the window are equally weighted. Conversely, the exponential smoothing methods place a higher weight on more recent data, and the weights decline exponentially to zero as returns become older.
• The rate at which the weights change, or smoothness, is determined by a parameter λ (known as the decay factor) raised to a power.

GARCH 

This is a time-series model used by analysts to predict time-varying volatility. Volatility is measured with a general GARCH(p,q) model using the following formula:

σ²_t =a + b₁r²_t-1,t + b₂r²_t-2,t-1 + …+b_pr²_{t-p, r-p+1}+c₁σ²_t-1+c₂σ²_t-2+…+c_qσ²_t-q

Where: parameters a,b₁ through b_p, and c₁ through c_q = parameters estimated using historical data with p lagged terms on historical returns squared & q lagged terms on historical volatility

NONPARAMETRIC APPROACHES FOR VAR #

HISTORICAL SIMULATION METHOD

Historical simulation is a procedure for predicting the value at risk by simulating or constructing the cumulative distribution function of assets return overtime.

Under the historical simulation, all returns are weighted equally based on the number of observations in the estimation window (1/K).

HYBRID APPROACH #

The hybrid approach uses historical simulation to estimate the percentiles of the return and weights that decline exponentially (similar to GARCH or RiskMetrics.

NONPARAMETRIC VS PARAMETRIC APPROACH #

Advantages of nonparametric methods compared to parametric methods:

• Nonparametric models do not require assumptions regarding the entire distribution of returns to estimate VaR.
• Fat tails, skewness, and other deviations from some assumed distribution are no longer a concern in the estimation process for nonparametric methods.
• Multivariate density estimation (MDE) allows for weights to vary based on how relevant the data is to the current market environment, regardless of the timing of the most relevant data.
• MDE is very flexible in introducing dependence on economic variables (called state variables or conditioning variables).
• Hybrid approach does not require distribution assumptions because it uses a historical simulation approach with an exponential weighting scheme.

Additional VaR LINEAR VS NON-LINEAR DERIVATIVES #

• A derivative is described as linear when the relationship between an underlying factor and the derivative is linear in nature. For example, an equity index futures contract is a linear derivative, while an option on the same index is non-linear. In general, the VaR of a long position in a linear derivative is VaRp = ΔVaRf, where VaRf is the VaR of the underlying factor and the derivative’s delta, Δ, is the sensitivity of the derivative’s price to changes in the underlying factor.
• The value of a nonlinear derivative is a function of the change in the value of the underlying asset and is dependent on the state of the underlying asset. A call option is a good example of a nonlinear derivative. The value of the call option does not increase (decrease) at a constant rate when the underlying asset increases (decreases) in value.

TAYLOR APPROXIMATION #

The Taylor Series of order two is represented mathematically as:

f (x) = f (x₀) + f ‘(x₀) (x – x₀ ) + 1/2 f “(x₀) (x – x₀)²

The first derivative tells us the delta, or slope of the line. The second derivative tells us the rate of change. The last term including the second derivative captures the convexity or curvature. This approximation is only useful for “well-behaved” quadratic functions of order two.

THE DELTA NORMAL & FULL REVALUATION METHODS #

The full revaluation approach calculates the VaR of the derivative by valuing the derivative based on the underlying value of the index after the decline corresponding to an x% VaR of the index.

The delta-normal approach calculates the risk using the delta approximation, which is linear or the delta-gamma approximation, f(x) = f (x₀) + f'(x₀)(x – x₀) + 1/2 f “(x₀)(x – x₀)² ,which adjusts for the curvature of the underlying relationship.

WORST CASE SCENARIO ANALYSIS #

The worst case scenario (WCS) assumes that an unfavourable event will occur with certainty. The focus is on the distribution of worst possible outcomes given an unfavourable event. An expected loss is then determined from this worst case distribution analysis. Thus, the WCS information extends the VaR analysis by estimating the extent of the loss given an unfavourable event occurs.

THE MONTE CARLO APPROACH #

The structured Monte Carlo (SMC) approach simulates thousands of valuation outcomes for the underlying assets based on the assumption of normality. The VaR for the portfolio of derivatives is then calculated from the simulated outcomes. The general equation assumes the underlying asset has normally distributed returns with a mean of μ, and a standard deviation of σ.  Advantage: It is able to address multiple risk factors by assuming an underlying distribution and modelling the correlations among the risk factors.

Disadvantage: In some cases it may not produce an accurate forecast of future volatility and increasing the number of simulations will not improve the forecast.

CORRELATIONS DURING CRISES

In times of crisis, correlations increase (some substantially) and strategies that rely on low correlations fall apart in those times. Certain economic or crisis events can cause diversification benefits to deteriorate in times when the benefits are most needed. A contagion effect occurs with a rise in volatility and correlation causing a different return generating process.

A simulation using the SMC approach is not capable of predicting scenarios during times of crisis if the covariance matrix was estimated during normal times. Unfortunately, increasing the number of simulations does not improve predictability in any way.

STRESS TESTING

Stressing the correlation is a method used to model the contagion effect that could occur in a crisis event.

• One approach for stress testing is to examine historical crisis events, such as the Asian crisis, October 1987 market crash, etc.
• 2nd approach is to analyse different predetermined stress scenarios.
• 3rd is the historical simulation approach. Under this approach, the entire data sample is used to identify “extreme stress” situations for different asset classes.