- +91 9096131868
- falconedufin@gmail.com
- All Day: 10:30 AM - 9:30 PM IST
C09 INTEREST RATES
ANNUAL COMPOUNDING VS. SEMIANNUAL COMPOUNDING #
If an account pays interest every six months, we say interest is compounded semi annually. Every three months represents quarterly compounding, and every month is monthly compounding. Use the following formula to find the future value of a bond using different compounding methods:
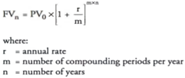
HOLDING PERIOD RETURN
The rate of return on a bond is as follows:
![]()
DERIVING DISCOUNT FACTORS FROM SWAP RATES #
In an interest rate swap, the fixed receiver (floating payer) “buys” the fixed leg, and the fixed payer (floating receiver) “sells” the fixed leg. Thus, we use fixed swap rates to derive discount factors. For this calculation, swap rates represent bond coupon payments and the swap notional amount represents the bond’s par value.
THE SPOT RATE CURVE #
A ^-period spot rate, denoted as z(t), is the yield to maturity on a zero-coupon bond that matures in f-years (assuming semi-annual compounding). The spot rate curve is the graph of the relationship between spot rates and maturity. For semi-annual coupon bonds, the f-year discount factor is related to the f-year spot rate as follows:

THE SPOT RATE CURVE #
Forward rates are interest rates that span future periods. It is the future yield on a bond. It is calculated using the yield curve. Bootstrapping is the process of computing forward rates from spot rates.
EFFECT OF MATURITY ON BOND PRICES & RETURN #
In general, bond prices will increase with maturity when coupon rates are above relevant forward rates. A bond’s return will depend on the duration of the investment and the relationship between spot and forward rates.
When short-term rates are above the forward rates utilized by bond prices, the investors who rolls over shorter-term investments will tend to outperform investors who invest in longer-term investments.
PAR RATES #
The par rate at maturity is the rate at which the present value of a bond equals its par value.
Assuming a par value of $1, par rate equation can be written as follows:
![]()
The sum of the discount factors: is known as the Annuity factor, AT.
![]()
PRICING A BOND USING A SPOT, FORWARD & PAR RATES #
Any bond can be split into a series of periodic cash flows. Each cash flow in isolation can be considered a STRIP. If the present value of each cash flow is computed and summed, the resulting number should be equivalent to the bond’s price. The appropriate discount rate for each cash flow is the spot rate. Discount factors can also be used because spot rates can be derived from discount factors.
Because spot rates and the implied forward rates are so closely related, it makes no difference which one is used to compute present values. A spot rate or a sequence of forward rates can be used to compute the present value.
YIELD CURVE SHAPES #
In general, bond prices will increase with maturity when coupon rates are above relevant forward rates. A bond’s return will depend on the duration of the investment and the relationship between spot and forward rates.
When short-term rates are above the forward rates utilized by bond prices, the investors who rolls over shorter-term investments will tend to outperform investors who invest in longer-term investments.
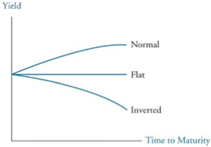
Historically, the yield curve has taken on three fundamental shapes:
A normal yield curve is one in which long-term rates are greater than short-term rates, so the curve has a positive slope . A flat yield curve represents the situation where the yield on all maturities is essentially the same. An inverted yield curve reflects the condition where long term rates are less than short-term rates, giving the yield curve a negative slope.
When the yield curve undergoes a parallel shift, the yields on all maturities change in the same direction and by the same amount.
When the yield curve undergoes a nonparallel shift, the yields for the various maturities change by differing amounts. The slope of the yield curve after a nonparallel shift is not the same as it was prior to the shift. Nonparallel shifts fall into two general categories: twists and butterfly shifts.
Yield curve twists refer to yield curve changes when the slope becomes either flatter or steeper. With an upward-sloping yield curve, a f l a t t e n i n g of the yield curve means that the spread between short- and long-term rates has narrowed. Conversely, a steepening of the yield curve occurs when spreads widen.
Yield curve butterfly shifts refer to changes in the degree of curvature. A positive butterfly means that the yield curve has become less curved.
Updated on February 16, 2022





